hanyeah

学完了KMP，发现还有比KMP更高效的算法，Boyer-Moore算法。这个比较复杂了。

原理看这篇：http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html

写的比较好，不过不够全面，没有具体实现。

可以结合这篇来看，上边有具体代码实现：http://blog.csdn.net/appleprince88/article/details/11881323

http://blog.csdn.net/sealyao/article/details/4568167

http://baike.baidu.com/link?url=KQ9Zf4plLYk1yUsJ-VVOGZ7DqljjgVIUdzbTU4tWuTzSAw6L8pZ_3Yr3jgL4F131d5zJlK-qNZIQwU3MRZgxYDo2GHVMJsV5PfXA-AxnQ_oo6_-sFrnWS3HQYsgbKSS9#4_2

Boyer-Moore算法的特点是从后往前匹配，按照“坏字符”规则，“好后缀”规则进行进行后移。

坏字符规则好理解，用于查找的表也好创建。

好后缀表比较麻烦，可以参考第二篇文章中的源码。仔细看看，“好后缀”规则其实和kmp中的方法很像，只不过kmp的next表是从前往后创建的， Boyer-Moore反过来了，从后往前。

function boyerMoore(s, t) {
    var n = s.length;
    var m = t.length;
    var i = 0;
    var j = 0;
    var bmBc = getBmBc(t);
    var bmGs = getBmGs(t);
    while (j <= n - m) {
        for (i = m - 1; i >= 0; i--) {
            if (t[i] != s[j + i]) {
                break;
            }
        }
        if (i < 0) {
            return j;
        } else {
            j += Math.max(i - (bmBc[t[i]] || -1), bmGs[i]);
        }
    }
    return - 1;
}

function getBmBc(t) {
    var arr = [];
    var len = t.length;
    for (var i = 0; i < len; i++) {
        arr[t[i]] = i;
    }
    return arr;
}
function suffix(t) {
    var arr = [];
    var m = t.length;
    arr[m - 1] = m;
    for (var i = m - 2; i >= 0; i--) {
        var q = i;
        while (q >= 0 && t[q] == t[m - 1 - i + q]) {
            q--;
        }
        arr[i] = i - q;
    }
    return arr;
}
function getBmGs(t) {
    var arr = suffix(t);
    var i = 0;
    var j = 0;
    var m = t.length;
    var bmGs = [];
    for (i = 0; i < m; i++) {
        bmGs[i] = m;
    }
    for (i = m - 1; i >= 0; i--) {
        if (arr[i] == i + 1) {
            for (; j < m - 1 - i; j++) {
                if (bmGs[j] == m) {
                    bmGs[j] = m - 1 - i;
                }
            }
        }
    }
    for (i = 0; i <= m - 2; i++) {
        bmGs[m - 1 - arr[i]] = m - 1 - i;
    }
    return bmGs;
}

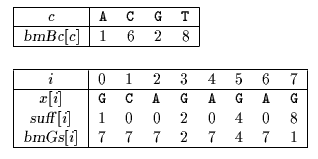
开发过程中方法的正确性可以用这个图中数据来验证。

好后缀算法没有看懂，有空继续研究。

结合前边的文章，总结如下：

suffix[i] = s 表示以i为边界，与模式串后缀匹配的最大长度，如下图所示，用公式可以描述：满足P[i-s, i] == P[m-s, m]的最大长度s。

Case1：模式串中有子串和好后缀安全匹配，则将最靠右的那个子串移动到好后缀的位置。继续进行匹配。

或

case2：模式串中没有子串匹配上好后缀，但找到一个最大前缀

case3：模式串中没有子串匹配上好后缀，且找不到一个最大前缀。