hanyeah

最长回文子串问题：给定一个字符串，求它的最长回文子串长度。

暴力解法：找到所有子串，验证是否是回文子串，时间复杂度是O(n^3)。

改进算法：遍历一遍字符串，求以每个字符为中心的回文子串长度，时间复杂度是O(n^2)。

用Manacher来解决最长回文子串问题，算法复杂度是O(n)。

Manacher算法属于动态规划，但是如果认为这样的算法才是动态规划，是对动态规划的误解，还会打击学习的积极性，动态规划只是在分治的基础上做了一些优化，《算法导论》里边讲的很好，也可以参考之前的一篇文章：动态规划。

参考：

https://www.cnblogs.com/grandyang/p/4475985.html

https://segmentfault.com/a/1190000003914228

https://segmentfault.com/a/1190000008484167

http://www.csie.ntnu.edu.tw/~u91029/index.html

算法利用回文子串左右对称的特性。

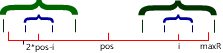
如上图，从左往右求每一个字符的回文子串，如果我们已经算过以pos为中心的回文子串，并记录下改回文子串的最右端maxR，当我们求之后的以i为中心（i<maxR）的回文子串的时候，可以直接读取i相对于pos的对称点的回文子串长度，如果i加上这个长度小于maxR的话，那么以i为中心的回文子串长度就是这个值，如果i加上这个长度大于等于maxR，那么以i为中心的回文子串长度至少是maxR-i，然后只需要判断以i为中心maxR以后的字符，之后pos更新为i，maxR更新为以i为中心的回文子串的最右端。如果i大于maxR的话，赋初始值，向后计算即可。

如果 maxR > i, 则 p[i] = min( p[2 * pos - i] , maxR - i ) 

否则，p[i] = 1

实际写代码的时候，用到了一些技巧，简化了代码量。当然，按照思路写if~else也没有问题。

manacher('122122');
manacher2('122122');
manacher('abbahopxp');
manacher2('abbahopxp');
function manacher(s){
	var a = ['#'];
	for(var i = 0; i < s.length; i++) {
		a.push(s.charAt(i));
		a.push('#');
	}
	var maxR = 0;
	var pos = 0;
	var resLen = 0;
	var resCenter = 0;
	var p = [];
	for(var i = 0; i < a.length; i++) {
		p[i] = maxR > i ? Math.min(p[2 * pos - i], maxR - i) : 1;
		while(a[i + p[i]] === a[i - p[i]]) {
			p[i]++;
		}
		if(maxR < i + p[i]) {
			maxR = i + p[i];
			pos = i;
		}
		if(resLen < p[i]) {
			resLen = p[i];
			resCenter = i;
		}
	}
	console.log('---------manacher start----------');
	console.log(s);
	console.log(a.join());
	console.log(p.join());
	console.log(resCenter, resLen);
	console.log(s.substr(Math.floor((resCenter + 1 - resLen) / 2), resLen - 1));
	console.log('---------manacher end----------');
}

function manacher2(s) {
	var a = ['#'];
	for(var i = 0; i < s.length; i++) {
		a.push(s.charAt(i));
		a.push('#');
	}
	var pos = 0;
	var maxR = 0;
	var p = [];
	for(var i = 0; i < a.length; i++){
		if (i < maxR) {
			var L = p[2*pos - i];
			if(i + L < maxR) {
				p[i] = L;
			} else {
				p[i] = maxR - i;
				pos = i;
				while(a[i + p[i]] === a[i - p[i]]){
					p[i]++;
				}
				maxR = i + p[i];
			}
		} else {
			p[i] = 1;
			pos = i;
			while(a[i + p[i]] === a[i - p[i]]){
				p[i]++;
			}
			maxR = i + p[i];
		}
		if (maxR === a.length) {
			break;
		}
	}
	console.log('---------manacher2 start----------');
	console.log(s);
	console.log(a.join());
	console.log(p.join());
	var mi = 0;
	for(var i = 1; i < p.length; i++) {
		if(p[i] > p[mi]) {
			mi = i;
		}
	}
	console.log(mi, p[mi]);
	console.log(s.substr(Math.floor((mi + 1 - p[mi]) / 2), p[mi] - 1));
	console.log('---------manacher2 end----------');
}

1. 先对字符串进行处理，插入一个原始字符串中不存在的字符（为了统一奇偶的情况，详见参考文章）。比如‘12321’插入‘#’后变成‘#1#2#3#2#1#’。

2. 初始化变量i=0,pos=0,maxR=0,p=[]。（p用来存储计算结果）

3. 计算以i为中心的回文子串长度。

1. 如果 maxR > i, 则 p[i] = min( p[2 * pos - i] , maxR - i ) ;否则，p[i] = 1

2. 继续向右扩展计算p[i]

3. 如果i+p[i]>maxR，更新maxR和pos
   

4. 如果i是字符串的结尾，结束，否则i++，跳转到3。

5. 通过p找到最大回文子串的位置和长度。