hanyeah

NB物理中画出来的导线，拖拽的时候，导线的变换效果很不错。

先看一下效果。

据说同事花了一个多月写出来的，当然还包括前边画线的部分。

核心代码如下：

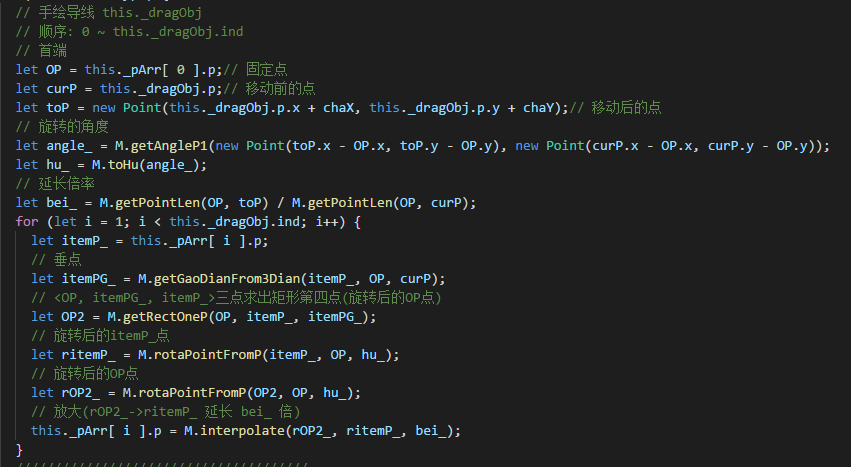
每句都加了注释，然而完全看不懂。

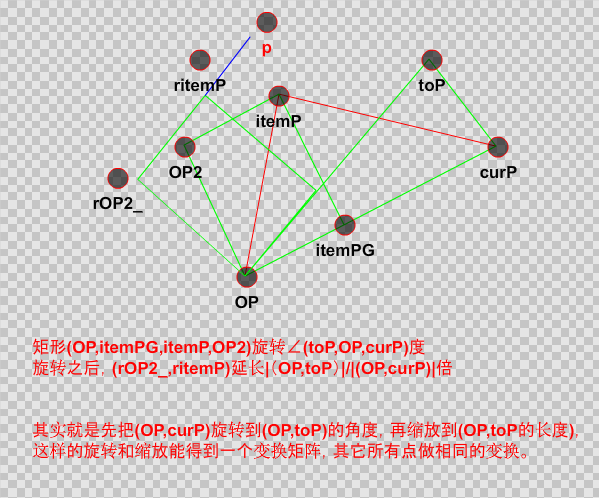
其实就是上面的操作。

还是很难懂，对不对。

用flash模拟的效果。

鼠标在上面移动，可以看效果，是不是很像。

其实原理很简单，就是做了一个旋转和一个方向上的缩放。

只是人为的把实现过程写复杂了。

可以通过矩阵操作，把旋转和缩放效果整体的变换矩阵求出来，然后对每一个点应用变换即可。

变换矩阵
|a,b|
|c,d|

缩放s
|s, 0|
|0, s|

旋转q
|cos(q), -sin(q)|
|sin(q),  cos(q)|

先缩放，再旋转
变换矩阵
旋转*缩放
|s*cos(q), -s*sin(q)|
|s*sin(q),  s*cos(q)|

先旋转，再缩放
变换矩阵
缩放*旋转
|s*cos(q), -s*sin(q)|
|s*sin(q),  s*cos(q)|

已知旋转的角度，缩放的倍数，就可以求出变换矩阵

上边的变换矩阵是
|a,  b|
|-b, a|
并且a * a + b * b = s * s

已知
|a,  b| |x0| = |x1|
|-b, a| |y0|   |y1|

a * x0 + b * y0 = x1  ①
-b * x0 + a * y0 = y1 ②

① * x0 + ② * y0
=> a * x0 * x0 + a * y0 * y0 = x1 * x0 + y1 * y0
=> a = (x1 * x0 + y1 * y0) / (x0 * x0 + y0 * y0)
① * y0 - ② * x0
=> b * y0 * y0 + b * x0 * x0 = x1 * y0 - y1 * x0
=> b = (x1 * y0 - y1 * x0) / (y0 * y0 + x0 * x0)

我们已知鼠标拖动的点上一次的坐标（x0,y0）以及当前坐标（x1,y1），就能求出a,b，也就是求出了变换矩阵，然后只需要遍历所有点，应用变换。

计算出变换矩阵，只需要8次乘除，3次加减，算上点的平移（坐标系平移）变换，需要再加2次加减操作。

变换矩阵应用到每一个点，一个点需要2次乘法，1次加法，加上点的坐标系变换，需要再加4次加减操作。

不需要算角度，也不需要算cos,sin.

性能上肯定有很大提升，毕竟原来算垂足，向量旋转，算角度，算长度，都是比较复杂的。

最重要的是，思路清晰，简洁。效果有几何解释，规范，容易理解。

上面的分析有误：缩放矩阵错误，x/y轴的缩放不应该一样。

这样的话，就不能用上面的结果了，上面的结果变换之后，x/y轴是等比缩放的，并不是沿着一个轴（x0,y0）缩放。

但是先计算变化，再对所有点应用变换的思想还是可以用的。（模型建好了，替换计算变换矩阵的方法，就可以得到不同的变换结果）

设变换矩阵是

|a, b|
|c, d|

应该有c/b 等于-d/a，后边可以验证一下。

(x0,y0)变换之后为(x1,y1)

可以得到两个方程

a * x0 + b * y0 = x1 ①

c * x0 + d * y0 = y1 ②

取与(x0, y0)垂直的向量(-y0, x0)，变换之后方向与(-y1,x1)一致，长度不变。

设变换之后为(-y1',x1')，有

y1' = y1 * d0 / d1

x1' = x1 * d0 / d1

其中d0为(x0, y0)的长度，d1为(x1, y1)的长度。

这样，可以得到另外两个方程:

-a * y0 + b * x0 = -y1' ③

-c * y0 + d *x0 = x1' ④

① * y0 + ③ * x0 消掉a 得：

b = (x1 * y0 - y1' * x0) / (x0 * x0 + y0 * y0) ⑤

② * y0 + ④ * x0 消掉c 得：

d = (y1 * y0 + x1' * x0) / (x0 * x0 + y0 * y0) ⑥

⑤带入① 求出a

a = (x1 - b * y0) / x0

⑥带入② 求出c

c = (y1 - d * y0) / x0

变换矩阵参数abcd全求出来了。

x0 等于0的时候，公式不适用，怎么办？

我们可以用消掉bd来求出ac。

① * x0 - ③ * y0 消掉b 得：

a = (x1 * x0 + y1' * y0) / (x0 * x0 + y0 * y0)

② * x0 - ④ * y0 消掉d 得：

c = (y1 * x0 - x1' * y0) / (x0 * x0 + y0 * y0)

当然，我们可以先把x轴和y轴换一换，计算完之后再对计算结果做一下变换，具体怎么变换还要分析一下。先不做了。