最近学习过程中,看到了环绕数,其中提到了判断点在多边形内的方法。记录一下。
网上搜索“点在多边形内”,可以得到好多文章,这里就不在重复介绍了。
网上文章千篇一律,都会介绍射线法,我们只看射线法。
射线法是说:过目标点做一条直线(两条反方向的射线),每条射线与多边形边的交点数量都是奇数,则点在多边形内,否则在多边形外部。
不难理解,实现起来也不难。
只是,并没有说的很明白。什么时候适用,为什么适用,什么时候不适用。
《复分析可视化方法》作者: [美] 尼达姆 著 ; 齐民友 译, 出版社: 人民邮电出版社。第7章中介绍了环绕数的概念。
还是数学比较严谨,程序员或者做技术的,只要能用就不会深究,不过了解一下还是有好处的。
首先,我们要判断点在多边形内还是外,需要先定义什么是内,什么是外。
一般人的反应是:这还需要定义。
看一下下面这个图,就知道为什么要定义了。
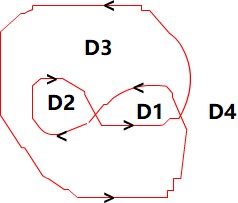
D1/D2/D3/D4中的点,哪个在多边形内,哪个在多边形外?如果没有定义,不同人,甚至一个人,不同时刻,给出的答案都是不一样的。
为什么我们平时没有这种感觉,或者,网上提到的方法,也没有定义内外,还都能用呢?
这是因为网上提到的方法,默认多边形是“简单环路”。
实际当中,我们也很少用到复杂环路,但是了解为什么还是有好处的。
按照书上给出的内外的定义,D1/D3中的点,是在多边形内,D2/D4是在多边形外。
根据环绕数的定义,D2/D4的环绕数是0,D3的环绕数是1,D1的环绕数是2。
对于简单环路,环绕数要么是0,要么是1,所以问题简化了,网上提到的方法适用。
对于复杂回路,环绕数存在大于1的情况,就要复杂一点了。
射线法,其实和书上给出的方法是一致的,只是省略了一些细节(没有考虑方向,一加一减)。
有兴趣可以下载电子书,看一看,电子书搜索就能下载到。
flash中多边形的填充规则,非零环绕规则、奇-偶环绕规则,也是和环绕数相关的。了解了环绕数,填充规则也就理解了。
非零环绕数规则和奇-偶规则(Non-Zero Winding Number Rule & Odd-even Rule) - 简书 (jianshu.com)
网上的文章没有讲环绕数的概念,所以看起来很高大上,很复杂。学习一下环绕数的概念,理解起来就很简单了。
这些东西就跟魔术似的,不了解底层原理,感觉好神秘,了解了底层原理,就不那么神秘了。
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。