动态规划(dynamic programming)与分治方法相似,都是通过组合子问题的解来求解原问题(在这里,“programming”指的是一种表格法,并非编写计算机程序)。分治方法将问题划分为互不相交的子问题,递归的求解子问题,再将它们的解组合起来,求出原问题的解。动态规划应用于子问题的解重叠的情况,即不同的子问题具有公共的子子问题。在这种情况下,分治算法会做许多不必要的工作,它会反复地求解那些公共子问题。而动态规划算法对每个子子问题只求解一次,将其保存在一个表格中,从而无需每次求解一个子子问题的解时都重新计算,避免了不必要的计算工作。
动态规划方法通常用来求解最优化问题,这类问题可以有很多可行解,每个解都有一个值,我们希望寻找具有最优值(最小值或最大值)的解。我们称这样的解为问题的一个最优解(an optimal solution),而不是唯一最优解(the optimal solution),因为可能有多个解都达到最优值。
我们通常按如下4个步骤来设计一个动态规划算法:
刻画一个最优解的结构特征。
递归的定义最优解的值。
计算最优解的值,通常采用自底向上的方法。
利用计算出的信息构造一个最优解。
钢条切割问题:给定一段长度为n英寸的钢条和一个价格表pi (i=1,2,...,n),求切割钢条方案,使得收益rn最大。
一般,对于rn(n≥1),我们可以总结出钢条的最优切割收益公式:
rn=max(pn, r1+rn-1 ,r2+rn-2,...,rn-1+r1)
第一个参数对应不切割。其他n-1个参数对应另外n-1种方案:对每个i=1,2,3,...,n-1,首先将钢条切割为长度为i和n-i的两段,接着求解这两段的最优切割收益ri和rn-i,求和。
除上述方法外,可以找到一种相似的但更为简单的递归求解方法:我们将钢条从左边切割下长度为i的一段,只对右边剩下的长度为n-i的一段继续进行切割(递归求解),对左边的一段则不再进行切割。即问题分解的方式为:将长度为n的钢条分解为左边开始一段,以及剩余部分继续分解的结果。
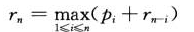
自顶向下递归实现:
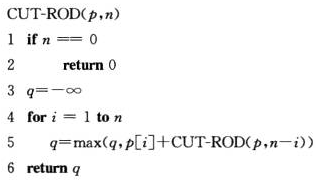
朴素递归算法之所以效率很低,是因为它反复求解相同的子问题。动态规划方法仔细安排求解顺序,对每个子问题只求解一次,并将结果保存下来。随后再次需要子问题的解时,只需要查找保存的结果,而不必重新计算。因此,动态规划方法是付出额外的内存空间来节省计算时间,是典型的是空权衡(time-memory trade-off)的例子。
动态规划有两种等价的实现方法。
带备忘录的自顶向下法。
自底向上法。
带备忘录的自顶向下法:
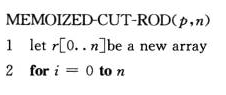

自底向上

var arr = [1,5,8,9,10,17,17,20,24,30,32,34,36,38,40,42,44,48,50,55,56,58,60,62];
function cut(n) {
if(n === 1) {
return arr[0];
}
var max = 0;
for(var i = 1; i < n; i++) {
max = Math.max(max, arr[i - 1] + cut(n - i));
}
return max;
}
var n = 20;
console.time('递归(n='+n+')');
console.log(n, cut(n));
console.timeEnd('递归(n='+n+')');
var a = [];
function cut1(n) {
if(!a[n]){
if(n === 1){
a[n] = arr[0];
} else {
var max = 0;
for(var i = 1; i < n; i++) {
max = Math.max(max, arr[i - 1] + cut(n - i));
}
a[n] = max;
}
}
return a[n];
}
var n = 20;
console.time('备忘录(n='+n+')');
console.log(n, cut1(n));
console.timeEnd('备忘录(n='+n+')');
function cut2(n) {
var a = [];
a[1] = arr[1];
for(var i = 2; i <= n; i++) {
var max = 0;
for(var j = 1; j < i; j++) {
max = Math.max(max, a[j] + a[i - j]);
}
a[i] = max;
}
return a[n];
}
var n = 20;
console.time('动态规划(n='+n+')');
console.log(n, cut2(n));
console.timeEnd('动态规划(n='+n+')');矩阵链乘法
给定一个n个矩阵的序列(矩阵链)<A1,A2,...,An>,如何安排计算的顺序,是的计算乘积所需要的标量乘法次数最少。
var arr = [
{r: 47, c: 25},
{r: 25, c: 8},
{r: 8, c: 46},
{r: 46, c: 14},
{r: 14, c: 47},
{r: 47, c: 42},
{r: 42, c: 31},
{r: 31, c: 42}
];
function calc(m, n) {
if (m === n) {
return 0;
}
var min = Infinity;
for(var i = m; i < n; i++) {
min = Math.min(min, calc(m, i) + calc(i + 1, n) + arr[m]['r'] * arr[i]['c'] * arr[n]['c']);
}
return min;
}
var n = arr.length;
console.time('递归');
console.log(calc(0, n - 1));
console.timeEnd('递归');
var a = {};
function calc1(m, n) {
var k = m+'_'+n;
if(typeof a[k] == 'undefined') {
if (m === n) {
a[k] = 0;
} else {
var min = Infinity;
for(var i = m; i < n; i++) {
min = Math.min(min, calc1(m, i) + calc1(i + 1, n) + arr[m]['r'] * arr[i]['c'] * arr[n]['c']);
}
a[k] = min;
}
}
return a[k];
}
var n = arr.length;
console.time('备忘录');
console.log(calc1(0, n - 1));
console.timeEnd('备忘录');
function calc2(n) {
var a = {};
for(var i = 0; i <= n; i++) {
for(var j = 0; j <= n - i; j++) {
var k = j+'_'+(j + i);
if(i === 0) {
a[k] = 0;
} else {
var min = Infinity;
for(var p = j; p < j + i; p++) {
min = Math.min(min, a[j+'_'+p] + a[(p+1)+'_'+(j + i)] + arr[j]['r'] * arr[p]['c'] * arr[j+i]['c']);
}
a[k] = min;
}
}
}
var k = '0_'+n;
return a[k];
}
var n = arr.length;
console.time('动态规划');
console.log(calc2(n - 1));
console.timeEnd('动态规划');
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。