设计给了两张图,一张俯视图A,一张侧视图B,要把A上的点映射到B上,B上的点映射到A上。怎么做?
只有两张图
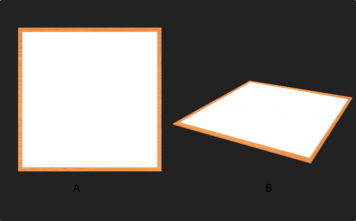
我们可以通过工具,获取每张图4个顶点的坐标,坐标之间必然存在映射关系,Pa = f(Pb),用矩阵表示,Pa = m*Pa。
我们要求m。
m用3*3的矩阵。
参考:https://www.cnblogs.com/faith0217/articles/5027490.html
透视变换(Perspective Transformation)用于解决仿射变换(Affine Transformation)无法改变形状内部的相对位置关系的问题。类似Photoshop中的“自由变换”功能,或者GIMP中的“透视”功能,都可以用透视变换矩阵来实现。
现在给定2个四边形:Poly1={{x1, y1}, {x2, y2}, {x3, y3}, {x4, y4}}、Poly2={{u1, v1}, {u2, v2}, {u3, v3}, {u4, v4}},求做一个透视变换Matrix,满足Poly1的点能够变形(Warp)到Poly2中的点。
透视变换矩阵的形式为:

显然,我们需要求解的只是矩阵中8个未知量;已知量包括四边形的4个顶点 x 2个坐标(x, y),一共是8个方程,数量刚刚好。对于每个顶点坐标,Poly1中的点总是通过下面的方程转换到Poly2中:
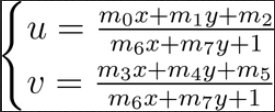
问题的关键在于,上面的公式需要求解非线性方程。因此,在解决Homography的问题上,常常用最小二乘法(Least Squares)求得参数估计。
其实稍加分析就不难发现,上面那个使用了分式的所谓“非线性方程”,实际上可以变形为:
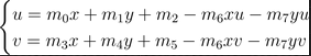
它居然变成了线性方程!看来一切试图用Newton迭代的算法都是没有必要的,因为我们可以用最简单的线性代数来解决:

下面是我用matlab计算的代码,mat就是我们要求的矩阵,顺便把mat的逆矩阵mat2也求出来,逆变换也有了。
没有matlab也没关系,运算不难,矩阵运算的库也不难找。
u1 = 0; v1 = 0; u2 = 1000; v2 = 0; u3 = 1000; v3 = 1000; u4 = 0; v4 = 1000; x1 = -375; y1 = 510; x2 = 254; y2 = 152; x3 = 1134; y3 = 304; x4 = 782; y4 = 828; a = [ x1, y1, 1, 0, 0, 0, -x1*u1, -y1*u1; 0, 0, 0, x1, y1, 1, -x1*v1, -y1*v1; x2, y2, 1, 0, 0, 0, -x2*u2, -y2*u2; 0, 0, 0, x2, y2, 1, -x2*v2, -y2*v2; x3, y3, 1, 0, 0, 0, -x3*u3, -y3*u3; 0, 0, 0, x3, y3, 1, -x3*v3, -y3*v3; x4, y4, 1, 0, 0, 0, -x4*u4, -y4*u4; 0, 0, 0, x4, y4, 1, -x4*v4, -y4*v4 ]; u = [u1,v1,u2,v2,u3,v3,u4,v4]'; m = a\u; mat = [m(1),m(2),m(3);m(4),m(5),m(6);m(7),m(8),1]; mat2 = inv(mat);
最后求出来结果是
mat = 0.622681800333835 -2.26554353140329 1388.93287614087 1.22602742955981 2.15410964579083 -638.835633268398 1.38327614714492e-06 0.00133144792441439 1 mat2 = 0.434597104229077 0.59516884730679 -223.411138468529 -0.177460145184904 0.0897866610409582 303.8391483172 0.000235677774164818 -0.000120369546353085 0.595763035916078
可以用mat*[x1,y1,1]来验证结果的正确性。
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。