hanyeah

物理实验里边经常会用到，测得一堆点，然后拟合一条直线。

之前学过梯度下降算法（关于梯度下降算法的的一些总结），也写过，但是直到现在都不理解，倒是能照着写出来。

如果只是拟合直线的话，可以用这个：最小二乘法 拟合平面直线。

可以看一下这个：https://www.zhihu.com/question/37031188

可以直接里边用到的结论：

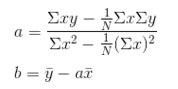
求出了a,b，直线也就有了y=ax+b。

用线性代数的知识，也可以解出ab。参考：http://open.163.com/movie/2010/11/P/U/M6V0BQC4M_M6V2AOJPU.html

写了个demo:

<canvas id = 'canvas' width = '1000' height = '600' style = 'width:1000px;height:600px;'></canvas>
<script type="text/javascript">
	var canvas = document.getElementById('canvas');
	var ctx = canvas.getContext('2d');
	var arr = [
		{x: 100, y: 100}
		, {x: 200, y: 220}
		, {x: 300, y: 300}
	];

	var ab = nihe(arr);
	console.log(ab);

	for(var i = 0; i < arr.length; i++){
		var o = arr[i];
		var w = 10;
		ctx.strokeStyle="#ff0000";
		ctx.strokeRect(o.x - w / 2, o.y - w / 2, w, w);
	}
	ctx.strokeStyle="#00ff00";
	ctx.beginPath();
	ctx.moveTo(0, getY(0));
	ctx.lineTo(1000, getY(1000));
	ctx.stroke();

	var ab = nihe2(arr);
	console.log(ab);

	function getY(x){
		return ab.a * x + ab.b;
	}

	function nihe(arr) {
		// https://blog.csdn.net/ouyangying123/article/details/53996403
		let len = arr.length;
		let xy = 0;
		let x2 = 0;
		let nx = 0;
		let ny = 0;
		for (let i = 0; i < len; i++) {
		  let o = arr[i];
		  xy += o.x * o.y;
		  nx += o.x;
		  ny += o.y;
		  x2 += o.x * o.x;
		}
		let a = (xy - nx * ny / len) / (x2 - nx * nx / len);
		let b = (ny - a * nx) / len;
		return {a: a, b: b};
	}

	function nihe2(arr){
		// ax + b = y
		// 求a，b
		// |x1 , 1|       |y1|
		// |x2 , 1|*|a| = |y2|
		// |x3 , 1| |b|   |y3|
		// ...
		// |xn , 1|       |yn|
		// 
		// 上边数组用Ax = b表示，A、b已知，求x。
		// 大多数时候无解。
		// 左乘A'(A的转置)，A'Ax = A'b，可使方程有解。
		// 
		let a = 0;
		let b = 0;
		let c = 0;
		let d = 0;
		let e = 0;
		let f = 0;
		let len = arr.length;
		for(let i = 0; i < len; i++){
			let o = arr[i];
			a += o.x * o.x;
			b += o.x;
			c += o.x;
			d += 1;
			e += o.x * o.y;
			f += o.y;
		}
		let y = (f * a - e * c) / (d * a - b * c);//(f - e * c / a) / (d - b * c / a);
		let x = (e - b * y) / a;
		return {a: x, b: y};
	}
</script>

如果只是拟合直线，第二种方法比较好，简单，准确。

第一种方法不止可以拟合直线，还可以拟合其他类型的曲线。目前用不到。