hanyeah

计算过椭圆中心的一条线段与椭圆的交点。

效果如下：

1、通过公式计算。

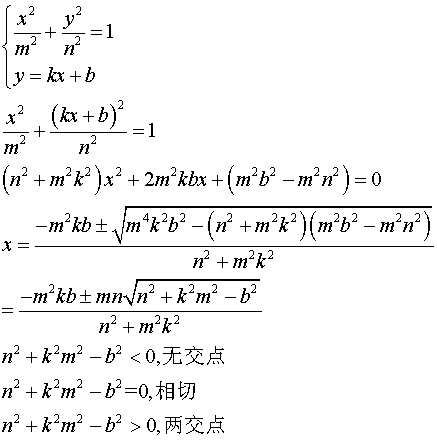
从网上找来的公式。

如果实际应用中椭圆的中心不在坐标原点，可以通过坐标变换将其移至坐标原点。

因为我们的线段过椭圆的中心，所以要么与椭圆有交点，要么无交点，不存在相切的情况；并且由于是线段，最多只有一个交点。

由于线段过椭圆中心（即坐标原点，因为我们平移了坐标轴），所以直线方程中，b=0。

线段的一个端点是固定的（坐标原点），判断椭圆和线段有没有交点可以更简单。只需要判断线段的另一个端点和椭圆的关系即可。点在椭圆内，无交点；点在椭圆上，端点就是交点；点在椭圆外，有交点。

判断点和椭圆的位置关系很简单，比如点的坐标是（x0,y0），将点的坐标代入椭圆方程。

x0²/m²+y0²/n²<1，点在椭圆内；

x0²/m²+y0²/n²=1，点在椭圆上；

x0²/m²+y0²/n²>1，点在椭圆外；

先判断椭圆和线段是否有交点，有交点且交点不是线段端点，再通过公式计算。

2、数值法

我们发现判断点和椭圆的位置关系很简单。

那么，如果线段和椭圆有交点，通过二分法可以很快的逼近交点坐标。查找过程如下图。

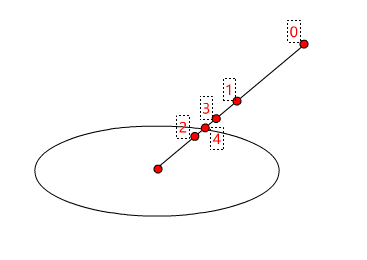
对比：

公式法得到的结果精确，速度快，但是核心公式相对来说比较复杂；

数值法只能得到近似解，速度相对较慢，但是核心公式简单。

代码如下：

package  {

	import flash.display.MovieClip;
	import flash.events.Event;
	import flash.geom.Point;

	/**
	 * @author hanyeah
	 */
	public class Main extends MovieClip {


		public function Main() {
			// constructor code
			addEventListener(Event.ENTER_FRAME, enterFrameHandler);
		}

		private function enterFrameHandler(e:Event):void 
		{
			var a:Number = 100;
			var b:Number = 50;
			var ox:Number=275;
			var oy:Number = 200;
			var p:Point = calEllipseLineIntersectPoint2(a, b, ox, oy, new Point(mouseX, mouseY));
			graphics.clear();
			graphics.lineStyle(1, 0x000000);
			graphics.drawEllipse(ox - a, oy - b, 2 * a, 2 * b);
			graphics.lineStyle(1, 0xff0000);
			graphics.moveTo(ox, oy);
			graphics.lineTo(mouseX, mouseY);
			if (p!=null){
				graphics.lineStyle(1, 0x00ff00);
				graphics.beginFill(0x00ff00, 1.0);
				graphics.drawCircle(p.x, p.y, 5);
				graphics.endFill();
			}

		}
		/**
		 * 线段和椭圆的交点。数值法。
		 * @param	a
		 * @param	b
		 * @param	offX
		 * @param	offY
		 * @param	p
		 * @return
		 */
		public function calEllipseLineIntersectPoint(a:Number, b:Number, offX:Number, offY:Number, p:Point):Point{
			var xM:Number = p.x - offX;
			var yM:Number = p.y - offY;
			var r:Number = calEllipsePointRelationship(a, b, xM, yM); 
			if (r<0){
				return null;
			}
			else if(r==0){
				return new Point(xM+offX,yM+offY);
			}
			else{
				var xL:Number = 0;
				var yL:Number = 0;
				var xR:Number = xM;
				var yR:Number = yM;
				while (true){
					xM = (xL + xR) / 2;
					yM = (yL + yR) / 2;
					if (distance(xL,yL,xR,yR)<1){
						break;
					}
					var r0:Number = calEllipsePointRelationship(a, b, xM, yM);
					if (r0==0){
						break;
					}
					else if (r0<0){
						xL = xM;
						yL = yM;
					}
					else{
						xR = xM;
						yR = yM;
					}
				}
				return new Point(xM+offX,yM+offY);
			}
			return null;
		}
		public function calEllipsePointRelationship(a:Number, b:Number,x0:Number,y0:Number):Number{
			return x0 * x0 / (a * a) + y0 * y0 / (b * b)-1;
		}
		public function distance(x0:Number,y0:Number,x1:Number,y1:Number):Number{
			return Math.sqrt((x0 - x1) * (x0 - x1) + (y0 - y1) * (y0 - y1));
		}
		/**
		 * 线段和椭圆的交点。公式法。
		 * @param	a
		 * @param	b
		 * @param	offX
		 * @param	offY
		 * @param	p
		 * @return
		 */
		public function calEllipseLineIntersectPoint2(a:Number, b:Number, offX:Number, offY:Number, p:Point):Point{
			var x1:Number = p.x - offX;
			var y1:Number = p.y - offY;
			var r:Number = calEllipsePointRelationship(a, b, x1, y1); 
			if (r<0){
				return null;
			}
			else if(r==0){
				return new Point(x1+offX,y1+offY);
			}
			else{
				if (x1 == 0){
					return new Point(0+offX,(y1>0?b:-b)+offY);
				}
				var k:Number = y1 / x1;
				var x2:Number = a * b / Math.sqrt(b * b + k * k * a * a);
				if (x1*x2<0){
					x2 =-x2;
				}
				return new Point(x2 + offX, k * x2 + offY);
			}
			return null;
		}
	}

}

源码打包下载