hanyeah-行列式计算

29

2018
09

行列式计算

维基百科:行列式。

行列式（determinant）是方阵的一个重要特征，常记作detA或者|A|，其包含了矩阵的很多重要信息。行列式为0，则矩阵不可逆，否则矩阵可逆，所以行列式可用来检验矩阵的可逆性。这篇文章主要介绍行列式的10个性质。
性质1：单位矩阵的行列式为1
性质2：如果交换矩阵的两行，则行列式的符号要取反。从这个性质我们可得出置换矩阵的行列式总是为1或-1，这取决于行交换的次数，行交换奇数次则为-1，偶数则为1。
性质3.1：如果用某数t乘以矩阵的一行，则行列式等于原行列式的t倍，即

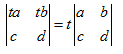
性质3.2：

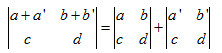
注意性质3两个性质都是关于行的线性，并不是整个矩阵的线性。而且我这里举例用了第一行，其实对其他行也是这样的性质，但是不管怎样不能同时组合第1行和第2行。
性质4：如果矩阵中有两行相等，那么行列式为0。假设m*n的矩阵A中，第2行和第3行相等，交换第2行和第3行，矩阵不变，但是根据性质2行列式符号会取反，也就是|A|=-|A|，则|A|=0，可以看到这跟结论有两个行相等的矩阵不可逆是一致的。
性质5：从矩阵的行k减去行i的l倍，行列式不会改变，即消元过程不改变行列式。根据性质3.2可证明这个性质：

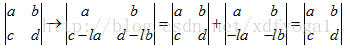
性质6：若矩阵中有一行是全0，则|A|=0。根据性质3.1，取t=0即可证明。
性质7：三角阵的行列式等于对角线元素乘积。现假设有上三角阵，这个矩阵很常见，因为通过消元总能得到这样的三角阵，det(U)=d1d2…dn，实际上matlab中也是根据这种方法求行列式的。假设主元都不为0，我们可以再对U向上消元，那么星号的地方都会被消为0，此时我们再利用性质3就可得到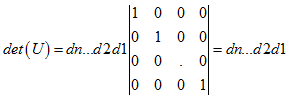：。但是如果主元位置上出现0，我们将得到全零行，利用性质6，则行列式为0。根据性质7，我们掌握了一种求解行列式的方法，即消元。比如对于我们所熟知的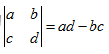，根据消元法有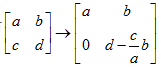，也能得出其行列式为ad-bc。

性质8：当且仅当A是奇异阵时，detA=0，否则就是非奇异阵。
性质9：detAB=det(A)det(B)。但是要注意行列式不具有加法性质，即不成立det(A+B)=detA+detB，性质9是非常有用的公式，比如说通过性质9我们可以求A-1的行列式，det（I）=1=det(A)det(A-1)，所以det(A-1)=1/det(A)；另外如果A是对角阵，比如A= ，那么根据性质9我们可以快速写出A^-1= ；此外还有det(A2)=(detA)2，既然前面提到det(A+B)=detA+detB不成立，那么如果矩阵乘以2行列式会变为多少呢？根据性质3.1有行列式det(2A)=2ndetA，其中A是n*n的矩阵，这就像求体积，对于一个立方体，令每条边乘以2，体积是2的n次方倍，对于三维的立方体，体积就是原来的8倍。
性质10：det(AT)=det(A)。这个性质表明前面所说的所有对行的性质，对列也是成立的。例如，如果存在全零列，行列式也为0。

$\det(A)=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}$

直接用代数表达式计算(需要用到全排列)。算法复杂度是O(n!)。

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define GET(a,n,i,j) *((int*)a + n*i + j)

// n的阶乘
int factorial(int n){
	int a = 1;
	while(n > 1){
		a *= n--;
	}
	return a;
}

// 交换两个整数
void swap(int *a, int *b){
	int temp;
	temp = *a;
	*a = *b;
	*b = temp;
}

// 全排列(包括逆序数的奇偶)
// 参考：https://www.jianshu.com/p/d4aaee236c8d
//       https://www.cnblogs.com/xianzhedeyu/p/3822946.html
void perm(int *r, int *t, int *a, int k, int n, int d){
	if(k < n){
		for(int i = k; i < n; i++){
			swap(&a[k], &a[i]);
			perm(r, t, a, k + 1, n, (i == k ? 1 : -1) * d);
			swap(&a[k], &a[i]);
		}
	} else {
		for(int i = 0; i < n; i++){
			r[*t] = a[i];
			*t = *t + 1;
		}
		r[*t] = d;
		*t = *t + 1;
	}
}

// 输出二维数组
void trace(int **a, int m, int n){
	for(int i = 0; i < m; i++){
		for(int j = 0; j < n; j++){
			// printf("%5d", *((int*)a + n*i + j));
			printf("%5d", GET(a, n, i, j));
		}
		printf("\n");
	}
}

// 输出全排列数组
void trace(int *r, int t, int n){
	int i = 0;
	while(i < t){
		for(int j = 0; j < n; j++){
			printf("%3d", *r++);
		}
		printf("\n");
		i+=n;
	}
}

// 输出一维数组
void trace(int *b, int n){
	for(int i = 0; i < n; i++){
		printf("%3d", b[i]);
	}
	printf("\n");
}

// 求行列式的值
int delt(int **a, int t, int *r, int n){
	int d = 0;
	int i = 0;
	while(i < t){
		int d0 = 1;
		for(int j = 0; j < n; j++){
			d0 = d0 * GET(a, n, j, *r++);
		}
		int a0 = *r++;
		d0 = d0 * a0;
		d += d0;
		i += n + 1;
	}
	return d;
}

void test(int n){
	int t = 0;
	int *r = (int *)malloc(factorial(n + 1)*sizeof(int));
	int a[n][n];
	int b[n];
	for(int i = 0; i < n; i++){
		b[i] = i;
	}
	for(int i = 0;i < n; i++){
		for(int j = 0; j < n; j++){
			if(abs(i - j) <= 1){
				a[i][j] = 1;
			} else {
				a[i][j] = 0;
			}
		}
	}
	printf("A = \n");
	trace((int **)a, n, n);
	// trace(b, n);
	perm(r, &t, b, 0, n, 1);
	// trace(r, t, n+1);
	int d = 0;
	d = delt((int **)a, t, r, n);
	printf("delt(A) = %d\n", d);
	free(r);
}

int main(){
	for(int i = 1; i <= 6; i++){
		test(i);
	}
	return 0;
}

也可以用代数余子式计算。

$M$ 关于元素 $m_{ij}$ 的代数余子式记作 $C_{ij}$ 。 $C_{ij}=(-1)^{(i+j)}\cdot M_{ij}$ 。

一个 $n$ $n$ 阶的行列式 $M$ $M$ 可以写成一行（或一列）的元素与对应的代数余子式的乘积之和，叫作行列式按一行（或一列）的展开。

$\det {M}=\sum _{i=1}^{n}m_{i;j}C_{i,j}$
$\det {M}=\sum _{j=1}^{n}m_{i;j}C_{i,j}$

这个公式又称拉普拉斯公式，把 $n$ $n$ 维矩阵的行列式计算变为了 $n$ $n$ 个 $n-1$ 维的行列式的计算。另一方面，拉普拉斯公式可以作为行列式的一种归纳定义：在定义了二维行列式后， $n$ $n$ 维矩阵的行列式可以借助拉普拉斯公式用 $n-1$ $n-1$ 维的行列式来定义。这样定义的行列式与前面的定义是等价的。

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define GET(a,n,i,j) *((int*)a + n*i + j)

// 输出二维数组
void trace(int **a, int m, int n){
	for(int i = 0; i < m; i++){
		for(int j = 0; j < n; j++){
			// printf("%5d", *((int*)a + n*i + j));
			printf("%5d", GET(a, n, i, j));
		}
		printf("\n");
	}
}

int cofactor(int **a, int n, int i, int j);
int det(int **a, int n);

// 代数余子式
int cofactor(int **a, int n, int i, int j){
	if(n == 1){
		return 1;
	}
	int si = ((i + j) & 0x1) == 1 ? -1 : 1;
	int n1 = n - 1;
	int c[n1][n1];
	int ii,jj;
	for(int ic = 0; ic < n1; ic++){
		for(int jc = 0; jc < n1; jc++){
			ii = ic < i ? ic : ic + 1;
			jj = jc < j ? jc : jc + 1;
			c[ic][jc] = GET(a, n, ii, jj);
		}
	}
	int r = det((int **)c, n1);
	return si * r;
}

// 行列式值
int det(int **a, int n){
	if(n == 1){
		return GET(a, n, 0, 0);
	}
	int r = 0;
	int aij;
	int cij;
	for(int i = 0; i < n; i++){
		aij = GET(a, n, i, 0);
		cij = cofactor(a, n, i, 0);
		r += aij * cij;
	}
	return r;
}

void test01(){
	int n = 4;
	int a[4][4] = {{1,1,0,0},{1,1,1,0},{0,1,1,1},{0,0,1,1}};
	int r = det((int **)a, n);
	printf("A = \n");
	trace((int **)a, n, n);
	printf("det(A) = %d", r);
}

void test(int n){
	int a[n][n];
	for(int i = 0;i < n; i++){
		for(int j = 0; j < n; j++){
			if(abs(i - j) <= 1){
				a[i][j] = 1;
			} else {
				a[i][j] = 0;
			}
		}
	}
	int r = det((int **)a, n);
	printf("A = \n");
	trace((int **)a, n, n);
	printf("det(A) = %d\n", r);
}

int main(){
	for(int i = 1; i <= 6; i++){
		test(i);
	}
	return 0;
}

算法复杂度是O(n!)。

计算行列式的值是一个常见的问题。最简单的方法是按照定义 $\det(A)=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}$ 计算或按照拉普拉斯公式进行递归运算。这样的算法需要计算 $n!$ 次的加法，复杂度是指数函数。在实际的计算中只能用于计算阶数很小的行列式。注意到拉普拉斯公式的性质，如果一行或一列里面有很多个0，那么就可以把行列式按这一行或一列展开，这时数值为零的系数所对应的代数余子式就不必计算了，因为最后要乘以0，这样就可以简化计算。然而更加简便的算法是利用高斯消元法或LU分解法，把矩阵通过初等变换变成三角矩阵或三角矩阵的乘积来计算行列式的值。这些算法的复杂度都是 $n^{3}$ 级别，远远小于直接计算的复杂度。

如果一个算法可以在 ${\mathit {O}}(n^{s})$ 时间内算出矩阵乘法，那么可以构造出一种 ${\mathit {O}}(n^{s})$ 时间内的行列式求值算法。这说明求矩阵的行列式的值和矩阵的乘法有相同的复杂度。于是，通过分治算法或者其它的方法，可以达到比 ${\mathit {O}}(n^{3})$ 更好的结果。比如，存在复杂度 ${\mathit {O}}(n^{2.376})$ 的行列式求值算法。

Tags: 行列式计算

发布:hanyeah | 分类:算法 | 评论:0 | 浏览:

发表评论:

◎欢迎参与讨论，请在这里发表您的看法、交流您的观点。

hanyeah

专注于AS

29

201809

行列式计算

发表评论:

2018
09