hanyeah

二叉搜索树（Binary Search Tree），（又：二叉查找树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉搜索树。

实现以下方法：

• 先序遍历

• 总序遍历

• 后序遍历

• 查找

• 后继

• 前驱

• 插入

• 删除

其它都很容易实现，删除是最难的，删除的时候要用到后继。

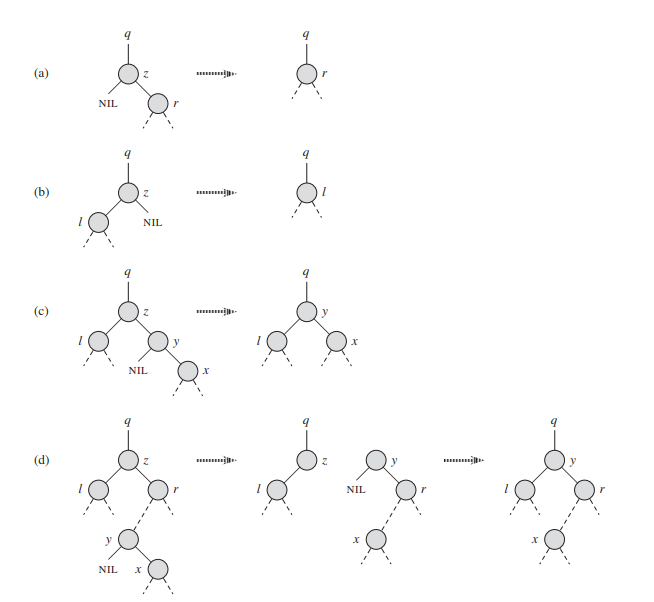
实现代码如下：

var t = {};
for(var i = 0; i < 10; i++){
	var k = Math.floor(Math.random()*20);
	treeInsert(t, {key:k});
	console.log("插入：", k);
}
treeInsert(t, {key:10});
console.log(t);
console.log("中序遍历：");
inOrderTreeWalk(t.root);
var a = treeSearch(t.root, 10);
treeDelete(t, a);
console.log("中序遍历：");
inOrderTreeWalk(t.root);


function inOrderTreeWalk(x){
	if(x){
		inOrderTreeWalk(x.left);
		console.log(x.key);
		inOrderTreeWalk(x.right);
	}
}

function preOrderTreeWalk(x){
	if(x){
		console.log(x.key);
		preOrderTreeWalk(x.left);
		preOrderTreeWalk(x.right);
	}
}

function postOrderTreeWalk(x){
	if(x){
		postOrderTreeWalk(x.left);
		postOrderTreeWalk(x.right);
		console.log(x.key);
	}
}

function treeSearch(x, k){
	if(!x || x.key == k){
		return x;
	}
	if(k < x.key){
		return treeSearch(x.left, k);
	}
	return treeSearch(x.right, k);
}

function iteractiveTreeSearch(x, k){
	if(x && x.key != k){
		if(k < x.key){
			x = x.left;
		} else{
			x = x.right;
		}
	}
	return x;
}

function treeMinimum(x){
	while(x.left){
		x = x.left;
	}
	return x;
}

function treeMaximum(x){
	while(x.right){
		x = x.right;
	}
	return x;
}

function treeSuccessor(x){
	if(x.right){
		return treeMinimum(x.right); 
	}
	var y = x.parent;
	while(y && x == y.right){
		x = y;
		y = y.parent;
	}
	return y;
}

function treePredecessor(x){
	if(x.left){
		return treeMaximum(x.left);
	}
	var y = x.parent;
	if(y && x == y.left){
		x = y;
		y = y.parent;
	}
	return y;
}

function treeInsert(t, z){
	var y = null;
	var x = t.root;
	while(x){
		y = x;
		if(z.key < x.key){
			x = x.left;
		}
		else {
			x= x.right;
		}
	}
	z.parent = y;
	if(!y){
		t.root = z;
	}
	else if(z.key < y.key){
		y.left = z;
	} else {
		y.right = z;
	}
}

function transPlant(t, u, v){
	if(!u.parent){
		t.root = v;
	} else if(u == u.parent.left){
		u.parent.left = v;
	} else {
		u.parent.right = v;
	}
	if(v){
		v.parent = u.parent;
	}
}

function treeDelete(t, z){
	if(!z.left){
		transPlant(t, z, z.right);
	} else if(!z.right){
		transPlant(t, z, z.left);
	} else{
		y = treeMinimum(z.right);
		if(y.parent!=z){
			transPlant(t,  y, y.right);
			y.right = z.right;
			y.right.parent = y;
		}
		transPlant(t, z, y);
		y.left = z.left;
		y.left.parent = y;
	}
}

https://github.com/hanyeah/lianxi/tree/master/算法导论/12