红黑树(Red Black Tree) 是一种平衡二叉搜索树。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色或红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根节点是黑色。
性质3 每个叶节点(NIL节点,空节点)是黑色的。
性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
了解平衡二叉树的两个基本操作:左旋、右旋。

插入
新插入的节点都是叶节点,如果破坏了树的性质,就从新插入的节点开始,通过左旋右旋操作,来保持树的性质,这样可能会导致上面的节点不满足树的性质,往上冒泡,继续操作,直到所有节点都满足树的性质。
红黑树插入元素时,只会破坏性质2或者性质4,破坏性质2的时候,节点肯定是根节点,直接把节点的颜色设置为Black就行,麻烦的是破坏性质4的时候的处理。
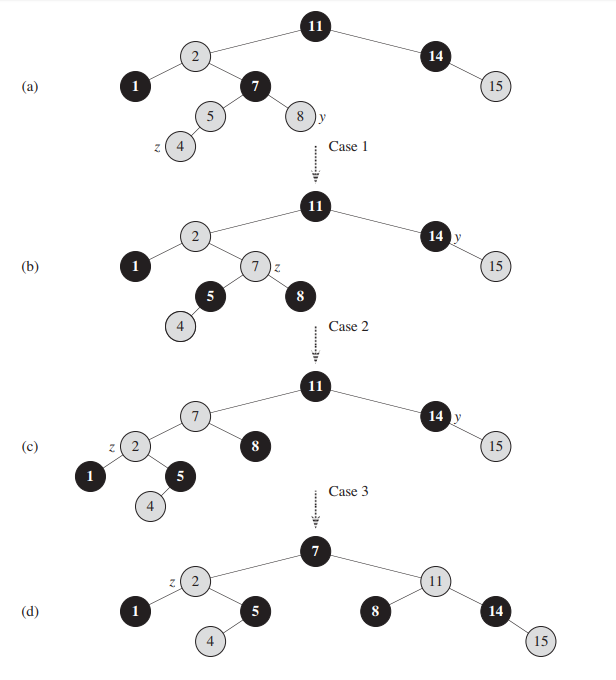
破坏性质4的时候,分成3种情况,1、叔节点是红色;2、叔节点是黑色,当前节点是父节点的左(右)孩子,父节点是祖父节点的右(左)孩子,(当前节点、父节点、祖父节点不在一条线上);3、叔节点是黑色,当前节点是父节点的左(右)孩子,父节点是祖父节点的左(右)孩子,(当前节点、父节点、祖父节点在一条线上);
处理方式:1、改变父节点、叔节点、祖父节点的颜色,祖父节点作为当前节点;(会变成2或3)
2、父节点作为当前节点,然后左旋(右旋),(会变成3)
3、改变父节点、祖父节点颜色,右旋(左旋)。
删除
删除时,和普通搜索二叉树一样,只是删除过程中需要额外记录一些信息,删除之后,可能会破坏性质1、2、4,需要通过改变颜色,左旋右旋来保持红黑树的性质。
有4种情况:1、x的兄弟节点w是红色的;2、x的兄弟节点w是黑色的,而且w的两个子节点都是黑色的;3、x的兄弟节点w是黑色的,w的左孩子是红色的,w的有孩子是黑色的;4、x的兄弟节点w是黑色的,w的右孩子是红色的。
处理方式:
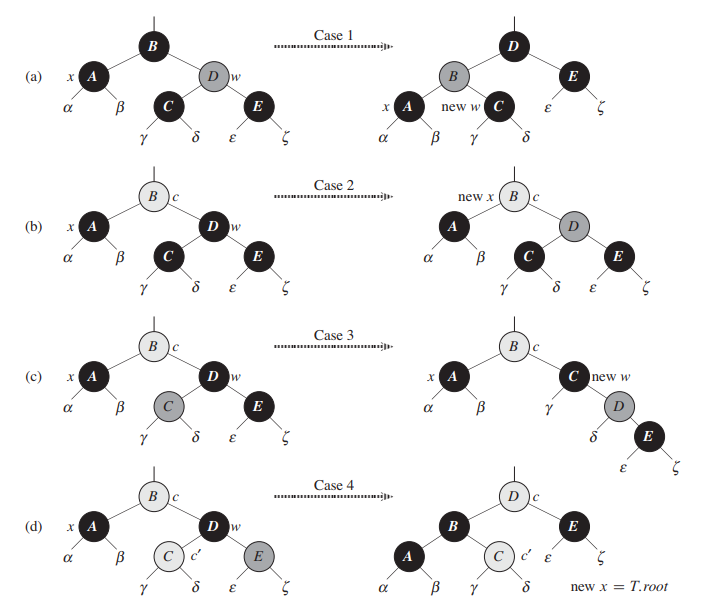
实现代码如下:
<canvas id = "canvas" width="1000" height="600" style="width:1000px;height:600px;"></canvas>
<script>
// 用canvas将树可视化
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');
function drawTree(t){
ctx.clearRect(0,0,1000,600);
drawNode(t.root, 30, 30);
}
function drawNode(node, x, y){
if(!node.key){
return {x: x, w: 30};
}
var o1 = drawNode(node.left, x, y + 30);
var o2 = drawNode(node.right, o1.x + o1.w / 2, y + 30);
var x = (o1.x + o2.x) / 2;
ctx.strokeStyle=node.color=='black'?"#000000":"#ff0000";
ctx.beginPath();
ctx.arc(x,y,10,0,2*Math.PI);
ctx.stroke();
ctx.beginPath();
ctx.moveTo(x, y);
ctx.lineTo(o1.x, y+30);
ctx.moveTo(x, y);
ctx.lineTo(o2.x, y+30);
ctx.stroke();
ctx.strokeText(node.key+"",x,y);
return {x: x, w: o1.w+o2.w};
}
</script>
<script>
// 测试红黑树
var t = {};
t.nil = {color:'black'};
t.root = t.nil;
var a = [];
console.log(a);
var n = 20;
for(var i = 0; i < n; i++){
var k = 1 + Math.floor(Math.random()*n);
a.push(k);
// console.log('插入:',k);
// rbInsert(t, {key: k});
}
// drawTree(t);
// console.log(t);
// console.log("中序遍历:");
// inOrderTreeWalk(t.root);
// 删除测试
/*while(a.length){
var o = treeSearch(t.root, a.pop());
rbDelete(t, o);
console.log("中序遍历:");
inOrderTreeWalk(t.root);
}*/
// 插入
var i = 0;
var delay = 1000;
setTimeout(charu, delay);
function charu(){
var k = a[i];
console.log('插入:',k);
rbInsert(t, {key: k});
drawTree(t);
i++;
if(i<n){
setTimeout(charu, delay);
} else {
i=0;
console.log("中序遍历:");
inOrderTreeWalk(t.root);
setTimeout(shanchu, delay);
}
}
function shanchu(){
var o = treeSearch(t.root, a[i]);
rbDelete(t, o);
drawTree(t);
i++;
if(i<n){
setTimeout(shanchu, delay);
}
}
/*
// 找BUG
a = [6, 3, 1, 8, 4, 8, 9, 3, 9, 6];
test();
function test(){
t = {};
t.nil={color:'black'};
t.root = t.nil;
var n = 0;
let loop = ()=>{
rbInsert(t,{key:a[n]});
n++;
if(n<a.length){
setTimeout(loop, 3000);
};
drawTree(t);
};
setTimeout(loop, 3000);
}*/
</script>
<script type="text/javascript">
function inOrderTreeWalk(x){
if(x != t.nil){
inOrderTreeWalk(x.left);
console.log(x.key);
inOrderTreeWalk(x.right);
}
}
function preOrderTreeWalk(x){
if(x != t.nil){
console.log(x.key);
preOrderTreeWalk(x.left);
preOrderTreeWalk(x.right);
}
}
function postOrderTreeWalk(x){
if(x != t.nil){
postOrderTreeWalk(x.left);
postOrderTreeWalk(x.right);
console.log(x.key);
}
}
function treeSearch(x, k){
if(!x || x.key == k){
return x;
}
if(k < x.key){
return treeSearch(x.left, k);
}
return treeSearch(x.right, k);
}
function leftRotate(t, x){
var y = x.right;
x.right = y.left;
if(y.left!=t.nil){
y.left.parent = x;
}
y.parent = x.parent;
if(x.parent == t.nil){
t.root = y;
} else if(x == x.parent.left){
x.parent.left = y;
} else {
x.parent.right = y;
}
y.left = x;
x.parent = y;
}
function rightRotate(t, y){
var x = y.left;
y.left = x.right;
if(x.right!=t.nil){
x.right.parent = y;
}
x.parent = y.parent;
if(y.parent == t.nil){
t.root = x;
} else if(y == y.parent.left){
y.parent.left = x;
} else {
y.parent.right = x;
}
x.right = y;
y.parent = x;
}
function rbInsert(t, z){
var y = t.nil;
var x = t.root;
while(x!=t.nil){
y = x;
if(z.key < x.key){
x = x.left;
} else {
x = x.right;
}
}
z.parent = y;
if(y == t.nil){
t.root = z;
} else if(z.key < y.key){
y.left = z;
} else {
y.right = z;
}
z.left = t.nil;
z.right = t.nil;
z.color = 'red';
rbInsertFixUp(t, z);
}
function rbInsertFixUp(t, z){
while(z.parent.color=='red'){
if(z.parent == z.parent.parent.left){
var y = z.parent.parent.right;
if(y.color=='red'){
z.parent.color = 'black';
y.color = 'black';
z.parent.parent.color = 'red';
z = z.parent.parent;
} else{
if(z == z.parent.right){
z = z.parent;
leftRotate(t, z);
}
z.parent.color = 'black';
z.parent.parent.color = 'red';
rightRotate(t, z.parent.parent);
}
} else {
var y = z.parent.parent.left;
if(y.color == 'red'){
z.parent.color = 'black';
y.color = 'black';
z.parent.parent.color = 'red';
z = z.parent.parent;
} else {
if(z == z.parent.left){
z = z.parent;
rightRotate(t, z);
}
z.parent.color = 'black';
z.parent.parent.color = 'red';
leftRotate(t, z.parent.parent);
}
}
}
t.root.color = 'black';
}
function rbTransplant(t, u, v){
if(u.parent==t.nil){
t.root = v;
} else if(u==u.parent.left){
u.parent.left = v;
} else {
u.parent.right = v;
}
v.parent = u.parent;
}
function treeMinimum(x){
while(x.left != t.nil){
x = x.left;
}
return x;
}
function treeMaximum(x){
while(x.right != t.nil){
x = x.right;
}
return x;
}
function rbDelete(t, z){
var y = z;
y.originalColor = y.color;
if(z.left == t.nil){
x = z.right;
rbTransplant(t, z, z.right);
} else if(z.right == t.nil){
x = z.left;
rbTransplant(t, z, z.left);
} else {
y = treeMinimum(z.right);
y.originalColor = y.color;
x = y.right;
if(y.parent == z){
x.parent = y;
} else {
rbTransplant(t, y, y.right);
y.right = z.right;
y.right.parent = y;
}
rbTransplant(t, z, y);
y.left = z.left;
y.left.parent = y;
y.color = z.color;
}
if(y.originalColor == 'black'){
rbDeleteFixUp(t, x);
}
}
function rbDeleteFixUp(t, x){
while(x!=t.root && x.color=='black'){
if(x == x.parent.left){
var w = x.parent.right;
if(w.color=='red'){
w.color = 'black';
x.parent.color = 'red';
leftRotate(t, x.parent);
w = x.parent.right;
}if(!w.right||!w.left)debugger
if(w.left.color == 'black' && w.right.color == 'black'){
w.color = 'red';
x = x.parent;
} else{
if(w.right.color == 'black'){
w.left.color = 'black';
w.color = 'red';
rightRotate(t, w);
w = x.parent.right;
}
w.color = x.parent.color;
x.parent.color = 'black';
w.right.color = 'black';
leftRotate(t, x.parent);
x = t.root;
}
} else {
var w = x.parent.left;
if(w.color=='red'){
w.color = 'black';
x.parent.color = 'red';
rightRotate(t, x.parent);
w = x.parent.left;
}if(!w.right||!w.left)debugger
if(w.right.color == 'black' && w.left.color == 'black'){
w.color = 'red';
x = x.parent;
} else{
if(w.left.color == 'black'){
w.right.color = 'black';
w.color = 'red';
leftRotate(t, w);
w = x.parent.left;
}
w.color = x.parent.color;
x.parent.color = 'black';
w.left.color = 'black';
rightRotate(t, x.parent);
x = t.root;
}
}
}
x.color = 'black';
}
</script>
发表评论:
◎欢迎参与讨论,请在这里发表您的看法、交流您的观点。