hanyeah

问题：已知透镜的焦距，求一条光线经过透镜之后，出射光线方向。

对于凸透镜，我们知道，过焦平面上同一点的两条光线经过透镜之后会变成平行光；光路可逆，平行光经过透镜以后，一定相交于焦平面上一点。

对于凹透镜，我们知道，延长线过出射侧焦平面上同一点的两条光线经过透镜之后会变成平行光，光路可逆，平行光经过透镜以后，反向延长线一定相交于焦平面上一点。

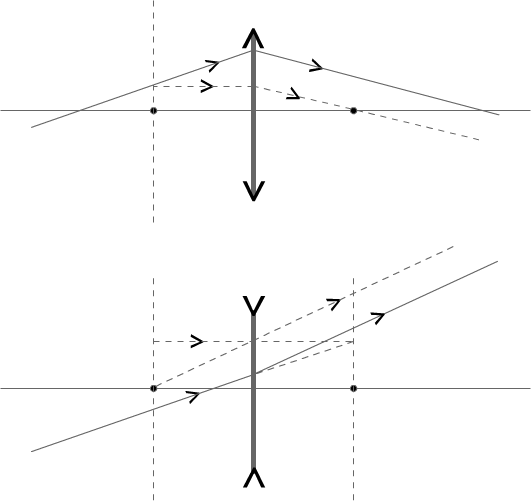
我们按照下面的方式做辅助线。只需要求出虚线出设光线的方向，也就得到了出射光线的方向（平行，方向向量一样）。

对于凸透镜，只需要求出入射光线和焦平面的交点即可。

对于凹透镜，只需要求出入射光线延长线和出射侧焦平面的交点即可。

实现代码如下：

/**
   * 凸透镜计算
   * 原理
   * 假设从左侧入射（右侧原理一样）
   * 1、求入射光线和左焦点所在竖直直线的交点
   * 2、从求得的交点发射一条水平光线，经过透镜之后，一定过右侧焦点。(平行光，经过透镜之后，一定过焦点)
   * 3、很容易求得水平光线折射之后的方向。
   * 4、原入射光线经透镜折射之后的光线和3中的折射光线平行。（过焦点的光线，经过透镜之后，变平行）
   * @param sp 入射光线上一点
   * @param dir 入射光线方向
   * @param f 焦距
   * @return {OptPoint} 出设光线方向
   */
  protected _calcConvexLens(sp: OptPoint, dir: OptPoint, f: number): OptPoint {
    const n: number = dir.x > 0 ? -1 : 1; // 法线方向
    const f1: number = f * n; // 入射侧焦点
    const f2: number = -f * n; // 出射侧焦点
    // 求入射光线在入射侧焦点位置的y坐标y0.
    // sp.x + dir.x * t0 = f1;
    // sp.y + dir.y * t0 = y0;
    // => y0 = sp.y + dir.y * (f1 - sp.x) / dir.x
    const y0: number = sp.y + dir.y * (f1 - sp.x) / dir.x;
    return new OptPoint(-f1, -y0);
  }

  /**
   * 凹透镜计算
   * 原理
   * 假设从左侧入射（右侧原理一样）
   * 1、求入射光线和右焦点所在竖直直线的交点
   * 2、从入射侧发射一条水平光想，指向交点，经过透镜之后，反向延长线一定过左侧焦点。(平行光，经过透镜之后，反向延长线一定过焦点)
   * 3、很容易求得水平光线折射之后的方向。
   * 4、原入射光线经透镜折射之后的光线和3中的折射光线平行。（过焦点的光线，经过透镜之后，变平行）
   * @param t
   */
  public calcConcaveLens(): OptPoint {
    const sp: OptPoint = this.localRay.sp;
    const dir: OptPoint = this.localRay.dir;
    const n: number = dir.x > 0 ? -1 : 1; // 法线方向
    const f: number = this.data.f; // 焦距
    const f1: number = -f * n; // 入射侧焦点
    const f2: number = f * n; // 出射侧焦点
    // 求入射光线在出射侧焦点位置的y坐标y0.
    // sp.x + dir.x * t0 = f2;
    // sp.y + dir.y * t0 = y0;
    // => y0 = sp.y + dir.y * (f2 - sp.x) / dir.x
    const y0: number = sp.y + dir.y * (f2 - sp.x) / dir.x;
    return new OptPoint(f2, y0);
  }

我们发现，两个代码很像，而且，我们是不是可以把凹透镜看做一个焦距是负值的凸透镜呢。

我们把两个代码合并成一个：

protected calcLens(sp: OptPoint, dir: OptPoint, f: number): OptPoint {
  const n: number = dir.x > 0 ? -1 : 1; // 法线方向
  const f1: number = f * n; // 入射侧焦点
  // 求入射光线在入射侧焦点位置的y坐标y0.
  // sp.x + dir.x * t0 = f1;
  // sp.y + dir.y * t0 = y0;
  // => y0 = sp.y + dir.y * (f1 - sp.x) / dir.x
  const y0: number = sp.y + dir.y * (f1 - sp.x) / dir.x;
  if (f < 0) {
    return new OptPoint(f1, y0);
  }
  return new OptPoint(-f1, -y0);
}

再加上对于焦距为无穷大或者0的处理。最后算出的方向归一化。把参数中的点展开。最后得到：

/**
 * 凸透镜计算
 * 原理
 * 假设从左侧入射（右侧原理一样）
 * 1、求入射光线和左焦点所在竖直直线的交点
 * 2、从求得的交点发射一条水平光线，经过透镜之后，一定过右侧焦点。(平行光，经过透镜之后，一定过焦点)
 * 3、很容易求得水平光线折射之后的方向。
 * 4、原入射光线经透镜折射之后的光线和3中的折射光线平行。（过焦点的光线，经过透镜之后，变平行）
 *
 * 凹透镜计算
 * 原理
 * 假设从左侧入射（右侧原理一样）
 * 1、求入射光线和右焦点所在竖直直线的交点
 * 2、从入射侧发射一条水平光想，指向交点，经过透镜之后，反向延长线一定过左侧焦点。(平行光，经过透镜之后，反向延长线一定过焦点)
 * 3、很容易求得水平光线折射之后的方向。
 * 4、原入射光线经透镜折射之后的光线和3中的折射光线平行。（过焦点的光线，经过透镜之后，变平行）
 *
 * @param cx 入射光线上一点x坐标
 * @param cy 入射光线上一点y坐标
 * @param dx 入射光线方向x坐标
 * @param dy 入射光线方向y坐标
 * @param f 焦距
 * @return {OptPoint} 出设光线方向
 */
public static calcLens(cx: number, cy: number, dx: number, dy: number, f: number): OptPoint {
  let p: OptPoint;
  if (f === Infinity || f === -Infinity) {
    p = new OptPoint(dx, dy);
  } else {
    const n: number = dx > 0 ? -1 : 1; // 法线方向
    const f1: number = f * n; // 入射侧焦点
    // 求入射光线在入射侧焦点位置的y坐标y0.
    // cx + dx * t0 = f1;
    // cy + dy * t0 = y0;
    // => y0 = cy + dy * (f1 - cx) / dx
    const y0: number = cy + dy * (f1 - cx) / dx;
    if (f < 0) {
      p = new OptPoint(f1, y0);
    } else {
      p = new OptPoint(-f1, -y0);
    }
  }
  p.normalize();
  return p;
}

总共只有十几行代码。

对于透镜不在原点，或者旋转过的透镜，可以先做变换，把光线变换到透镜中心为原点，透镜方向为y轴的坐标系内，然后再计算，算完再反变换回去。