递增进位制法
这个算法是基于序列的递增进位制数。递增进位制数是指数字的进制随着位数的递增而递增。一般情况下,数字最右边的进制是2,次右边的进制是3,以此类推。n位递增进位制数一共包含n!个数字,所以它可以与全排列生成算法结合在一起。
递增进位制法
这个算法是基于序列的递增进位制数。递增进位制数是指数字的进制随着位数的递增而递增。一般情况下,数字最右边的进制是2,次右边的进制是3,以此类推。n位递增进位制数一共包含n!个数字,所以它可以与全排列生成算法结合在一起。
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。
动态规划(dynamic programming)与分治方法相似,都是通过组合子问题的解来求解原问题(在这里,“programming”指的是一种表格法,并非编写计算机程序)。分治方法将问题划分为互不相交的子问题,递归的求解子问题,再将它们的解组合起来,求出原问题的解。动态规划应用于子问题的解重叠的情况,即不同的子问题具有公共的子子问题。在这种情况下,分治算法会做许多不必要的工作,它会反复地求解那些公共子问题。而动态规划算法对每个子子问题只求解一次,将其保存在一个表格中,从而无需每次求解一个子子问题的解时都重新计算,避免了不必要的计算工作。
维基百科:行列式。
行列式(determinant)是方阵的一个重要特征,常记作detA或者|A|,其包含了矩阵的很多重要信息。行列式为0,则矩阵不可逆,否则矩阵可逆,所以行列式可用来检验矩阵的可逆性。这篇文章主要介绍行列式的10个性质。
性质1:单位矩阵的行列式为1
性质2:如果交换矩阵的两行,则行列式的符号要取反。从这个性质我们可得出置换矩阵的行列式总是为1或-1,这取决于行交换的次数,行交换奇数次则为-1,偶数则为1。
性质3.1:如果用某数t乘以矩阵的一行,则行列式等于原行列式的t倍,即
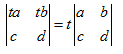
性质3.2:
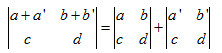
注意性质3两个性质都是关于行的线性,并不是整个矩阵的线性。而且我这里举例用了第一行,其实对其他行也是这样的性质,但是不管怎样不能同时组合第1行和第2行。
性质4:如果矩阵中有两行相等,那么行列式为0。假设m*n的矩阵A中,第2行和第3行相等,交换第2行和第3行,矩阵不变,但是根据性质2行列式符号会取反,也就是|A|=-|A|,则|A|=0,可以看到这跟结论有两个行相等的矩阵不可逆是一致的。
性质5:从矩阵的行k减去行i的l倍,行列式不会改变,即消元过程不改变行列式。根据性质3.2可证明这个性质:
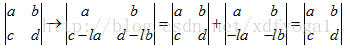
性质6:若矩阵中有一行是全0,则|A|=0。根据性质3.1,取t=0即可证明。
性质7:三角阵的行列式等于对角线元素乘积。现假设有上三角阵 ,这个矩阵很常见,因为通过消元总能得到这样的三角阵,det(U)=d1d2…dn,实际上matlab中也是根据这种方法求行列式的。假设主元都不为0,我们可以再对U向上消元,那么星号的地方都会被消为0,此时我们再利用性质3就可得到:
,这个矩阵很常见,因为通过消元总能得到这样的三角阵,det(U)=d1d2…dn,实际上matlab中也是根据这种方法求行列式的。假设主元都不为0,我们可以再对U向上消元,那么星号的地方都会被消为0,此时我们再利用性质3就可得到: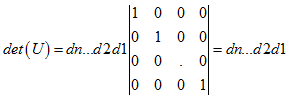 。但是如果主元位置上出现0,我们将得到全零行,利用性质6,则行列式为0。根据性质7,我们掌握了一种求解行列式的方法,即消元。比如对于我们所熟知的
。但是如果主元位置上出现0,我们将得到全零行,利用性质6,则行列式为0。根据性质7,我们掌握了一种求解行列式的方法,即消元。比如对于我们所熟知的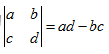 ,根据消元法有
,根据消元法有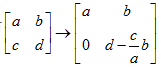 ,也能得出其行列式为ad-bc。
,也能得出其行列式为ad-bc。
性质8:当且仅当A是奇异阵时,detA=0,否则就是非奇异阵。
性质9:detAB=det(A)det(B)。但是要注意行列式不具有加法性质,即不成立det(A+B)=detA+detB,性质9是非常有用的公式,比如说通过性质9我们可以求A-1的行列式,det(I)=1=det(A)det(A-1),所以det(A-1)=1/det(A);另外如果A是对角阵,比如A= ,那么根据性质9我们可以快速写出A-1=
,那么根据性质9我们可以快速写出A-1= ;此外还有det(A2)=(detA)2,既然前面提到det(A+B)=detA+detB不成立,那么如果矩阵乘以2行列式会变为多少呢?根据性质3.1有行列式det(2A)=2ndetA,其中A是n*n的矩阵,这就像求体积,对于一个立方体,令每条边乘以2,体积是2的n次方倍,对于三维的立方体,体积就是原来的8倍。
;此外还有det(A2)=(detA)2,既然前面提到det(A+B)=detA+detB不成立,那么如果矩阵乘以2行列式会变为多少呢?根据性质3.1有行列式det(2A)=2ndetA,其中A是n*n的矩阵,这就像求体积,对于一个立方体,令每条边乘以2,体积是2的n次方倍,对于三维的立方体,体积就是原来的8倍。
性质10:det(AT)=det(A)。这个性质表明前面所说的所有对行的性质,对列也是成立的。例如,如果存在全零列,行列式也为0。
二叉树的遍历有三种方式:前序遍历、中序遍历、后序遍历,都是用递归方式实现的,很简单也很清晰。
同学问了一个问题,如何用非递归方式实现二叉树的遍历。